
Because it is possible to create cones using both for and while loops, I will go over the process for each.
The process for coding a cone is very similar to coding a cylinder, except you already know the x, y, w, and h values of one of the ellipses. Because these processes are so similar, I won't go into quite as much detail here, so if any parts of this tutorial are confusing, or you don't understand where some values are coming from, check out the cylinders tutorial for more information.
The idea behind this is that the computer is stacking circles on top of each other as they get smaller and smaller until they are so small that they're just a single point.


First, find the center position (x,y), width, and height of the base of the cone (shown here in blue), and the (x,y) position of the vertex (shown here in purple).
The first thing you need to do is find the difference between the x and y values of the center of the base and the vertex. We'll call these values distances and they should always be positive so subtract the smaller value from the larger one. In this example, the x distance is 0 (200-200) and the y distance is 300 (400-100).
Next, figure out how many ellipses need to be drawn to get from the base to the vertex or vice versa, which we'll call the totalSteps value. This value is equal to the larger of the x distance and the y distance. In this case, totalSteps equals 300, the y distance, because it is greater than 0, the x distance.
Then, you need to figure out how much each parameter of the ellipse–x, y, w, and h–changes with each iteration of the loop. We'll call these amounts steps. To do this, divide the x and y distances and the w and h values of the base ellipse by the totalSteps value. Here, the x step is 0 (0/300), the y step is 1 (300/300), the w step is 0.667 (200/300), and the h step is 0.1667 (50/300).
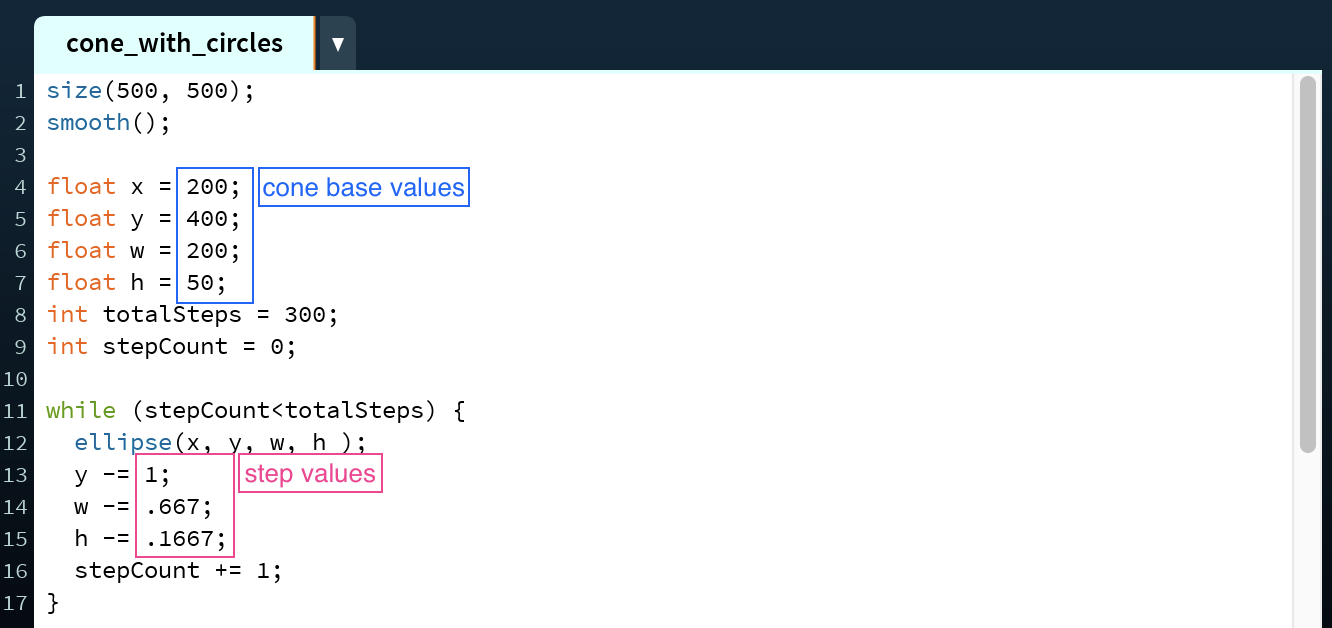
Regardless of whether you are using a for loop or a while loop, you will need to have variables for x (line 4), y (line 5), width (line 6), height (line 7), and stepCount (here instantiated on line 10), but may also have variables for the step value of each parameter if you choose. I include a variable for the totalSteps (line 8) to make it easier to keep track of. It's important to make the x, y, w, and h variables floats because the step values are frequently floats.
When setting up the for loop, have the loop variable keep track of how many times the loop has been iterated through so it can stop once the stepCount has reached the totalSteps value, increasing stepCount by 1 each time (line 10).
Before the loop is executed, figure out which way the cone is facing. If the base of the cone is facing towards you (meaning you can see the face of elliptical base), the starting x, y, w, and h values should be those of the base ellipse. However, if the cone base of the cone is facing away from you (meaning you are seeing the top of the cone and cannot see the face of the elliptical base), the starting x and y values should be those of the vertex and the starting w and h values should be 0. In this example, we'll focus on a cone whose base is facing you.
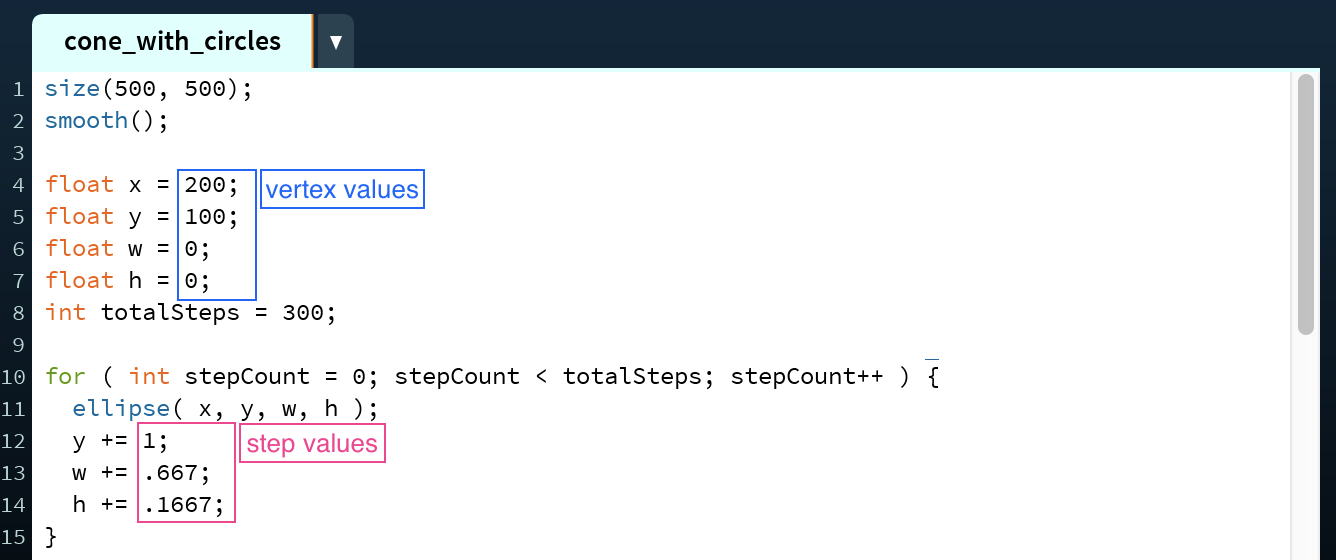
Within the for loop, draw an ellipse at position (x,y) with a width w and a height h (line 11). Then, update the variables that change based on their respective step values (lines 12 - 14). When doing this, make sure that the steps values are being added/subtracted appropriately: if the y value you are starting at is smaller than the y value you are ending at, add the y step value to y. Think through each variable like this to ensure the end result is what you want it to be.

To construct a cone using a while loop, update the stepCount (here instantiated on line 9) value by one with each iteration until it reaches the totalSteps value. As with the for loop, if the cone base is facing toards you–as it is here–the starting x, y, w, and h values should be those of the base ellipse; otherwise, the starting x and y values should be those of the vertex and the starting w and h values should be 0.

Within the loop body, draw an ellipse at position (x,y) with a width w and a height h (line 11). Then, update the variables that change based on their respective step values (lines 12 - 14). When doing this, make sure that the steps values are being added/subtracted appropriately: if the y value you are starting at is smaller than the y value you are ending at, add the y step value to y. Think through each variable like this to ensure the end result is what you want it to be. Because this is a while loop, it is also necessary to update the loop variable stepCount by 1 within the loop body (line 15).

This formula can be used to make many different kinds of cones.


Above is an example of a cone whose elliptical base can't be seen.


Above is another example of a cone whose elliptical base can be seen, but this cone's x, y, w, and h step values are all not equal to 0.

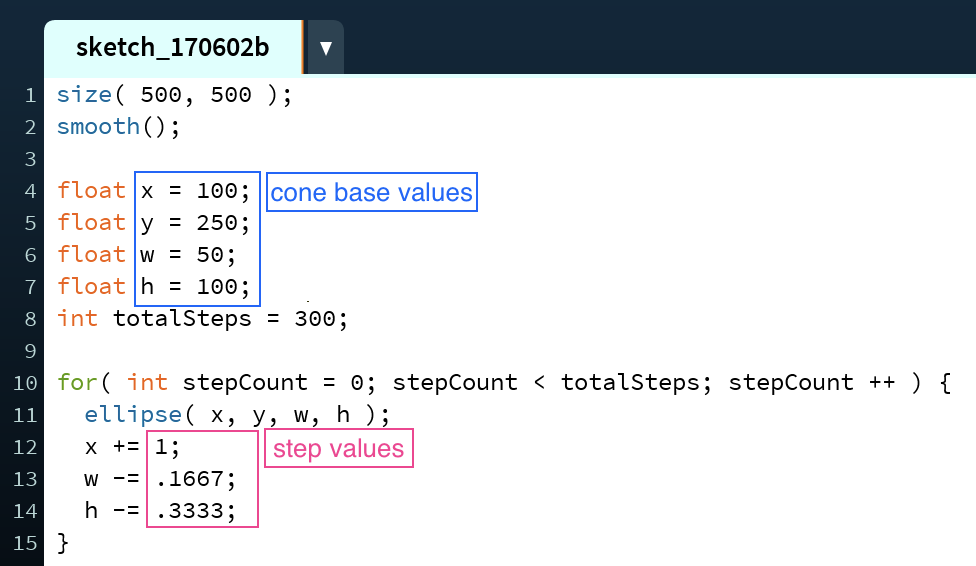
Above is another example of a cone whose elliptical base can't be seen, but this cone has an x step that is not equal to 0 and a y step that is.


Above is another example of a cone whose elliptical base can be seen, but this cone's vertex is below its elliptical base.