Finding Tiles Using Loops

You can make a tile pattern using only for- loops. If you would prefer to use an array to create the tile pattern, another tutorial will help you to do that.

This tutorial will show you how to make the diamond pattern as shown in the image below, but you can modify it to draw square tiles if that's what you prefer.

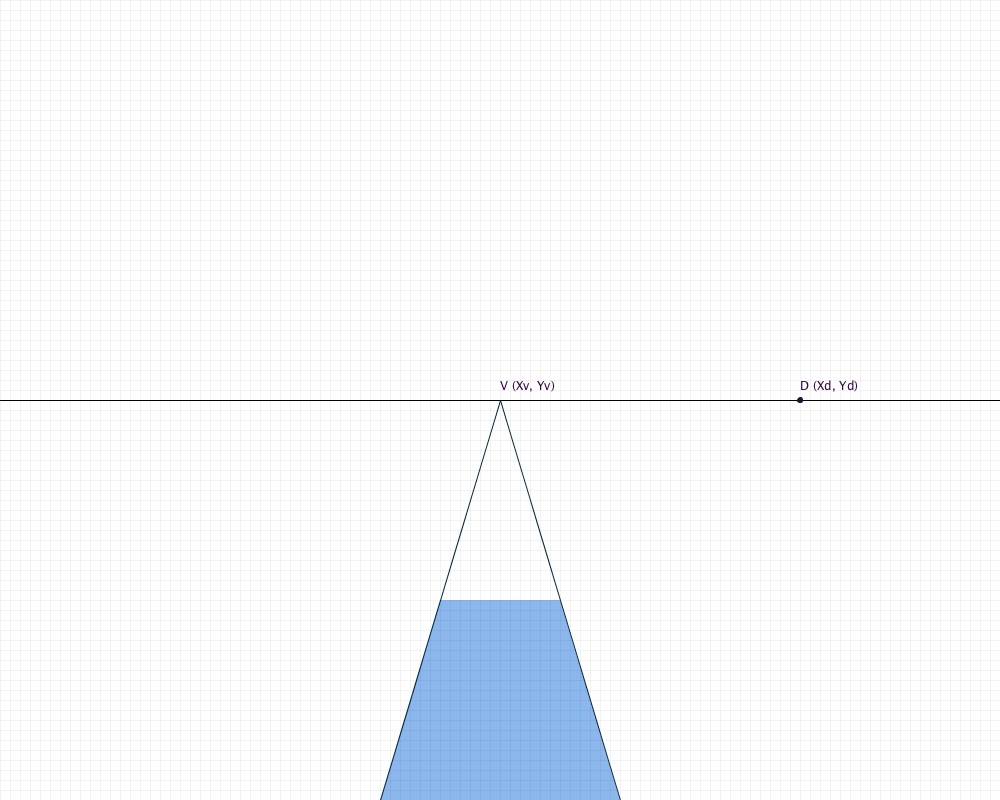
Before you begin drawing tiles, you will need to know a few things about your sketch. The first thing is the coordinates of a few points. The first is the vanishing point of the tiled floor. If you have a sketch on paper, you find this point by extending the two sides of your trapezoidal floor area until they intersect. This intersection is called the vanishing point. As shown in the image below, we denote the vanishing point as V. The y-value of V is also the height of the horizon line. Another point on the horizon line is D. You can find the coordinates of D from a perspective tiled floor sketch by extending a diagonal line through the corners of your tiles to intersect the horizon (for the purposes of this tutorial, we are extending these lines toward the right side of the sketch). Note that D has the same y-value as V.

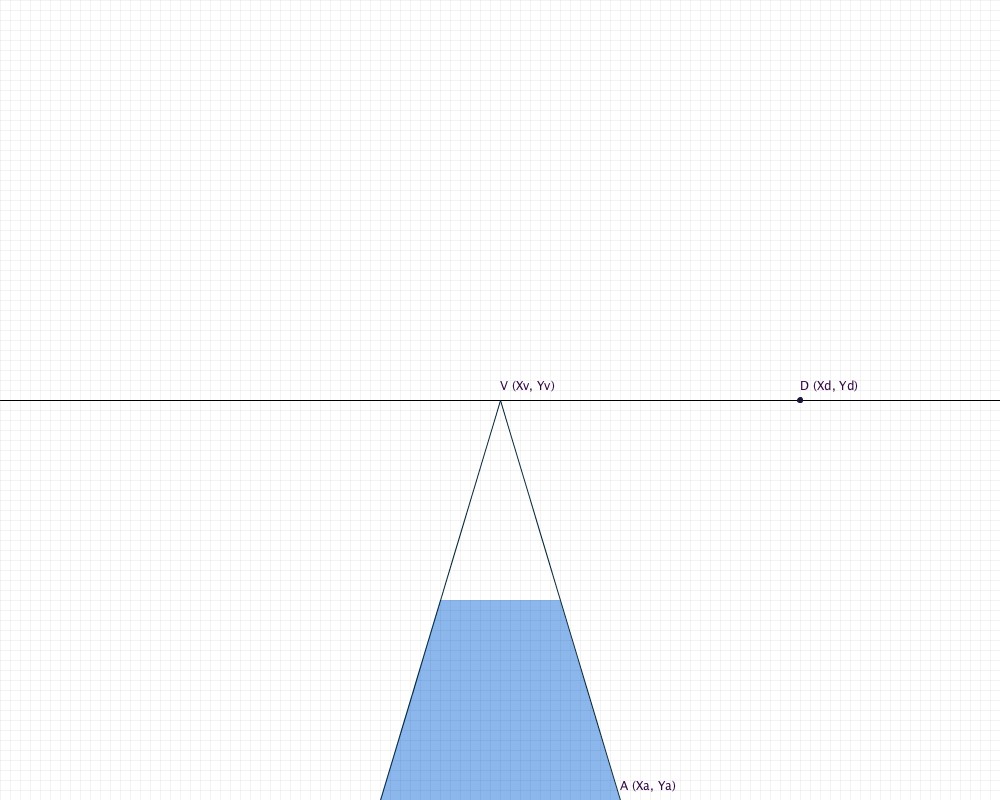
The last point you need to know is point A. Point A is the vertex at the bottom right of your floor.

You will also need to know two distances:

the distance between V and D, d
the width of one of your tiles, s

For this tutorial, we will be making our floor have a width of three tiles, so s is one third the length of our base.

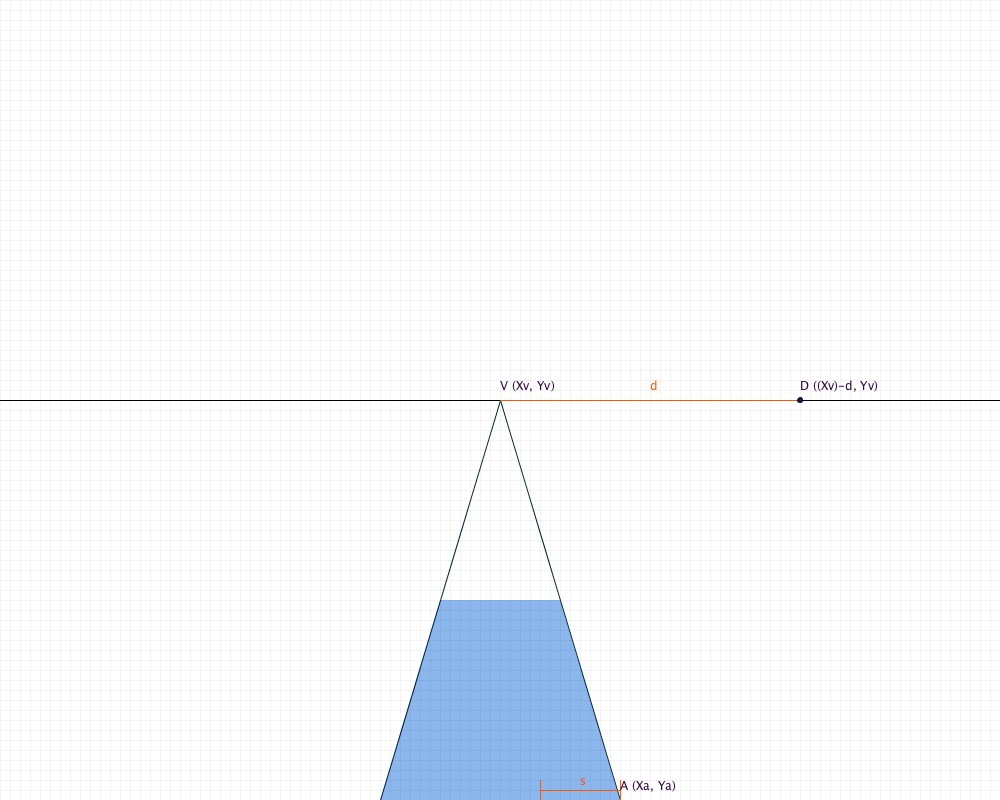
Drag your mouse and use the arrow keys with the sketch below to see how each variable affects the floor.

In order to draw the quadrilaterals which make up the diamonds, you will need the coordinates of all four points in each diamond. This will be done using parametric equations. You will need to use the coordinates of D and A to find these equations. The formula for a parametric equation given P₀ and P₁ is:

x = x₀ + t(x₁ - x₀)

y = y₀ + t(y₁ - y₀)

To find t, you will use the equation t = d / ((k * s) + d), where k is the number of tiles from A the point you are using is. Therefore:

x = x_{A_k} + (d / ((k * s) + d))(x_V-d - x_{A_k})

y = y_{A_k} + (d / ((k * s) + d))(y_V-d - y_{A_k})

It is now possible to create a diamond tile pattern using only loops. Since you want to create the pattern row by row, and you have h rows, your outer loop will iterate h times.

for (int k = 0; k < h; k++);

There are a few variables in each row that you will need to recalculate each time the loop iterates. These are:

t
the coordinates of the point on AV, x & y
the x-value of the point which falls on the line "parallel" to AV, xq
the width of a tile on the line which x and xq fall on, tileLength
and all of the above for the row k + 1; t2, x2, y2, xq2, and tileLength2

for (int k = 0; k < h; k++) {
  float t = d/((k * s) + d);
  float x = Xd + (t * (Xa - (k * s) - Xd));
  float y = Yd + (t * (Ya - Yd));
  float xq = (Xa - x) + Xb; //point on other side of the floor
  float tileLength = (x - xq) / w; //width of a tile from row k

  float t2 = d/(((k + 1) * s) + d);
  float x2 = Xd + (t2 * (Xa - ((k + 1) * s) - Xd));
  float y2 = Yd + (t2 * (Ya - Yd));
  float xq2 = (Xa- x2) + Xb;
  float tileLength2 = (x2 - xq2) / w; //width of a tile from row k + 1
}

Now that we have a loop the iterates through all of the rows, we want an inner loop to draw each tile in the current row. This loop will run w times. Within this loop, the four points required for creating the tile are located, and then the tile is drawn.

for (int k = 0; k < h; k++) {
  ...
  for (int i = 0; i < w; i++){
    float xv = x - (i * (tileLength));
    float xv2 = x2 - (i * (tileLength2));
    fill(...); //your tile color
    quad(xv, y, xv - tileLength, y, xv2, y2, xv2 - tileLength2, y2);
  }
}